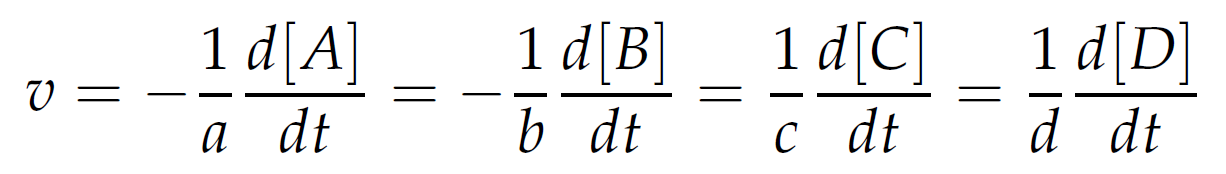Náplň podkapitoly:
1. Termodynamika
2. Kinetika
_
Termodynamika
Chemické reakce
Chemické reakce jsou děje, při nichž dochází k přeměně jedné skupiny sloučenin, reaktantů, na sloučeniny jiné, produkty. Reakcím odpovídají chemické rovnice:
aA + bB → cC + dD (1)
A a B jsou reaktanty, C a D produkty reakce. Malá písmena a, b, c, d označují stechiometrické koeficienty reakce, které nám říkají o hmotnostních poměrech chemických sloučenin účastnících se reakce. Pojem „rovnice” naznačuje existenci rovnosti mezi oběma stranami: při každé chemické reakci musí být zachována hmotnost, energie a elektrický náboj.
Podívejme se nyní na reakce mezi měďnými a železitými ionty v roztoku:
Cu+ + Fe3+ ↔ Cu2+ + Fe2+ (2)
Podobně jako většina reakcí v chemii (a téměř všechny v biochemii) je i tahle reakce vratná, což znamená, že může probíhat v obou směrech. K zastavení jejího průběhu dojde v bodě, kdy se určité množství železa zredukuje a určité množství mědi se zoxiduje. Hovoříme, že v tomto bodě dosáhla reakce rovnovážného stavu, tzn. že koncentrace reaktantů a produktů se v reakčním systému nemění. Tuto rovnováhu můžeme matematicky popsat použitím rovnovážné konstanty, Keq, která je definována jako podíl součinu rovnovážných koncentrací produktů a reaktantů (umocněných na jejich stechiometrické koeficienty):
K = [C]c[D]d / [A]a[B]b (3)
V našem příkladu:
K = [Cu2+][Fe2+] / [Cu+][Fe3+] (4)
Předpokládejme, že rovnovážná konstanta pro reakci (1) se rovná 1, tzn. že v rovnovážném stavu se součin koncentrací produktů a reaktantů shoduje. Jestliže do systému přidáme více sloučeniny A, porušíme tak nastolenou rovnováhu, a reakce se proto nastartuje ve směru, který se bude snažit opět obnovit původní stav. V našem případě bude látka A reagovat s látkou B za vzniku látek C a D tak dlouho, dokud se opět součiny koncentrací ([A][B] a [C][D]) nevyrovnají a nedosáhne se stavu nové rovnováhy. Toto pravidlo se nazývá Le Chatelierův princip.
Systém v rovnováze reaguje na změnu podmínek (tlaku, teploty, koncentrace) tak, aby tuto změnu potlačil.
Chemický potenciál
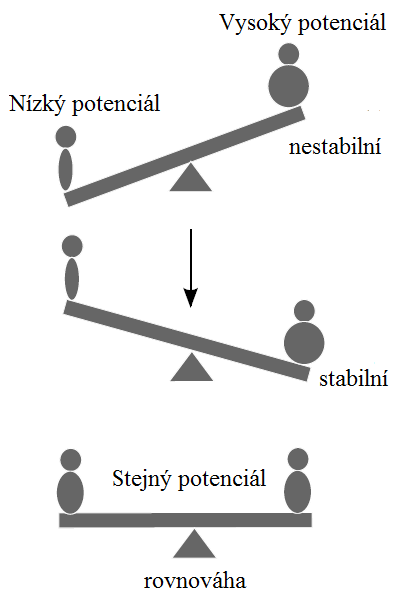
Můžeme se nyní zeptat, co způsobuje, že chemické reakce probíhají jako odpověď na změny v systému v jednom nebo opačném směru. Jako pomůcka nám pomůže analogie s houpačkou. Těžká osoba sedící na houpačce s někým lehčím se dříve či později nutně ocitne dole, zatímco dva lidé stejné hmotnosti skončí po čase v rovnovážném stavu na stejné úrovni nad zemí.
Jev můžeme vysvětlit pomocí potenciální energie obou lidí v gravitačním poli Země. Gravitační potenciální energie závisí na hmotnosti a poloze předmětu v gravitačním poli. Systém, jejž jsme použili v příkladu s houpačkou, se bude snažit minimalizovat svoji potenciální energii tím, že přesune těžší osobu co nejníže k zemi.
Podobně lze definovat chemický potenciál (μ) jako potenciální energii obsaženou v určitém množství látky, která se může během chemické reakce uvolnit. Analogicky k našemu příkladu s houpačkou jsou na obou stranách chemické rovnice látky s různým potenciálem. Pokud součet chemických potenciálů reaktantů převyšuje produktů produktů, bude reakce probíhat ve směru produktů, a naopak. Pokud se potenciály rovnají, systém dosáhl v rovnováhy.
Gibbsova energie
Rozdíl chemických potenciálů produktů a reaktantů je novou veličinou nazývanou změna Gibbsovy energie (ΔG). Z mnoha možných definic Gibbsovy energie jsou pro biochemii důležité zejména dvě:
1) Změna Gibbsovy energie je rovna maximálnímu množství (neobjemové) práce, kterou může systém vykonat
2) Změna Gibbsovy energie je mírou vychýlení se od rovnovážného stavu
První definice nám říká, že ΔG můžeme použít k předpovědi, jestli k reakci dojde a jestli ji lze využít jako zdroj energie pro jiné procesy (svalová kontrakce, přesun iontů přes membránu). Druhá definice vyjadřuje dva fakty:
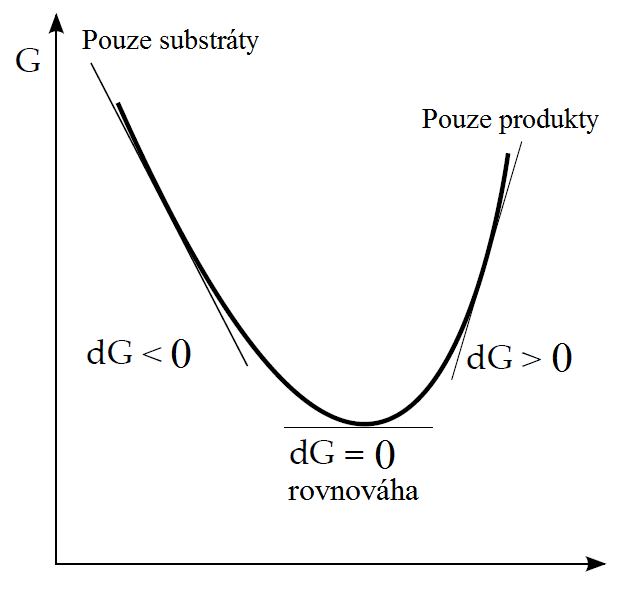
a) v rovnovážném stavu se ΔG rovná nule
b) změna koncentrací látek v systému, který není v rovnováze, změní (zvýší nebo sníží) ΔG.
Smysl Gibbsovy energie se dá ilustrovat i následujícím zobrazením.
Pokud reakce začne jen se směsí reaktantů, bude probíhat směrem k produktům tak dlouho, dokud zůstane ΔG negativní. Nabude-li chemický potenciál produktů stejné hodnoty jako u reaktantů, systém dosáhl stavu nejnižší energie a reakce se zastaví. Reakční směs je nyní v rovnováze. Nedá se předpokládat, že by reakce pokračovala dál, protože ΔG je v této části křivky pozitivní.
Změnu Gibbsovy energie můžeme také definovat prostřednictvím termodynamických veličin jako entalpie (H) a entropie (S):
ΔG = ΔH – TΔS (5)
ΔG < 0 – reakce probíhá spontánně
ΔG = 0 – rovnovážný stav
ΔG > 0 – reakce neprobíhá
Entalpie je energie uvolněná nebo spotřebovaná během reakce (negativní hodnota znamená uvolnění energie a naopak) a entropie je míra neuspořádanosti systému. Podle druhého zákona termodynamiky neuspořádanost (a tedy i entropie) všech uzavřených systémů narůstá.
Z rovnice (5) vyplývá, že chemická reakce může být poháněna (tzn. dosáhnout negativní ΔG) buď vhodnou (tedy negativní) změnou entalpie nebo dostatečným nárůstem entropie či oběma současně.
Z praktických důvodů je vhodné si definovat standardní podmínky, za nichž se ΔG a jiné veličiny změří, a poté je použít na výpočet skutečných situací. V chemii se považují za standardní podmínky tlak 1 atm (101 325 Pa), 25 °C (298.15 K) a 1 molární koncentrace všech látek. Veličiny, které v těchto podmínkách změříme, se označují indexem 0. Biochemici definují své standardní podmínky při pH = 7 (na rozdíl od pH = 0 v běžných chemických měřeních). Standardní veličiny jsou v biochemii značeny ‘.
Z tabulkových hodnot ΔG0 nebo ΔG0’ můžeme vypočítat ΔG pro jakoukoliv reakci pomocí rovnice:
ΔG = ΔG0 + RT ln ([C]c[D]d / [A]a[B]b) (6)
V rovnovážném stavu je ΔG rovné nule a [C]c[D]d / [A]a[B]b je rovné Keq. Rovnice (6) nabývá podoby:
ΔG = – RT ln Keq (7)
Prostřednictvím této rovnice pak můžeme vypočítat rovnovážnou konstantu z ΔG či naopak.
Snadná dostupnost hodnot ΔG0 může vést k nadužívání tabulek a k uspěchaným závěrům o nemožnosti průběhu reakce při nalezení pozitivních hodnot ΔG0 v tabulce. Tomu je ale třeba se vyhnout.
Podívejme se na příklad ze života. Metabolická dráha glykolýzy obsahuje krok, ve kterém dochází k přeměně glukóza-6-fosfátu na její izomer, fruktóza-6-fosfát. ΔG0‘ této reakce činí +1,7 kJ/mol. Znamená to tedy, že naše buňky prováděním této reakce každou sekundu našeho života porušují zákony termodynamiky?
Je důležité mít na paměti rozdíl mezi ΔG a ΔG0 či ΔG0‘. Jen ΔG nám může prozradit něco o termodynamickém profilu konkrétní reakce. Hodnoty ΔG0 a ΔG0‘ platí jen při zachování standardních podmínek, které ale jsou v přírodě zřídkakdy (jestli vůbec) přítomny. Abychom mohli posoudit pravděpodobnost, že k reakci dojde, musíme poznat skutečné koncentrace všech látek, jež se jí účastní. Činností enzymů dochází v našich buňkách k neustálému odstraňování fruktóza-6-fosfátu, a tak se jeho koncentrace udržuje na nízké úrovni. Celkové ΔG izomerizace Glc-6-P na Fru-6-P je díky tomu záporné (-2,5 kJ/mol). Tak mohou být i některé energeticky relativně nepříznivé reakce sdruženy s reakcemi energeticky příznivými. Pokud reakce přeměny A → B dosahuje rovnovážného stavu s nízkou koncentrací látky B (např. probíhá velmi špatně), můžeme ji sdružit s reakcí přeměny B → C, která naopak dosahuje rovnovážného stavu pouze při nízkých koncentracích B. Druhá reakce potom efektivně odstraňuje látku B tvořenou první reakcí a brání jí tak v dosažení rovnovážného stavu. V našem příkladu glykolýzy enzym fosfofruktokináza velmi efektivně fosforyluje Fru-6-P na fruktózu-1,6-bisfosfát, čímž zamezuje hromadění Fru-6-P, který by předchozí reakci brzdil.
Elektrochemická rovnováha
Chemické reakce, při nichž dochází ke změně oxidačních čísel prvků, se nazývají redoxní reakce. Při oxidaci se oxidační číslo zvyšuje, při redukci se snižuje. Tyto změny obvykle zahrnují přenos elektronů z jednoho atomu či molekuly na další.
Ponoříme-li zinkovou tyč do roztoku síranu zinečnatého, spustí se reakce, při které kovový zinek odevzdává dva elektrony a mění se na Zn2+, dokud se znovu nenastolí rovnováha. Proces vede k hromadění elektrického náboje, jejž označujeme jako elektrodový potenciál (E). Ten lze změřit nikoli přímo, ale jen jako rozdíl vůči jinému potenciálu. Rozdíl potenciálů známe jako napětí měřené ve voltech. Na překonání problému měření absolutního potenciálu vymysleli chemici malý trik: zvolili si jednu z elektrod a přidělili jí nulový potenciál. Nazývá se standardní vodíková elektroda (anglicky SHE – standard hydrogen electrode). Elektrodový potenciál (E) je tedy ve skutečnosti rozdíl potenciálů (někdy se proto označuje ΔE).
Je zjevné, že množství elektrického náboje, a tedy i hodnota elektrodového potenciálu budou souviset s rovnovážnou konstantou reakce. Ale jak? Vzpomeňme si, že ΔG odpovídá maximálnímu množství práce, kterou systém může vykonat. V elektrickém poli je práce konána přesouváním náboje přes rozdíl potenciálů (podobně jako je mechanická práce konána přesouváním hmoty v gravitačním poli). Vztah mezi ΔG a E pak vyjadřuje rovnice:
ΔG = – nFE (8)
Platí zde, že n = počet elektronů přenesený v redoxní reakci; F = Faradayova konstanta (rovná se náboji 1 molu elektronů, přibližně 9.6485309 x 104 C.mol-1); E = celkový rozdíl potenciálů mezi oběma poloreakcemi.
Pro standardní elektrodový potenciál můžeme vztah odvodit obdobně:
ΔE0 = (RT / nF) lnK (9)
Bez standardních podmínek má tato tzv. Nernstova rovnice (9) tvar:
E = E0 – (RT / nF) ln [redukované]/[oxidované] (10)
Jak lze tyto reakce použít k výpočtu toho, zda bude, nebo nebude určitá redoxní reakce probíhat? Rozhodující hodnotu představuje, tak jako předtím, hodnota ΔG příslušné reakce. Lze ji vypočítat z reakce (8).
Uvažujme reakci:
Zn + Cu2+ ↔ Zn2+ + Cu (11)
Dvě poloreakce, které probíhají, jsou:
Zn ↔ Zn2+ + 2e– (12)
Cu2+ + 2e– ↔ Cu (13)
Zinek se oxiduje, zatímco měď redukuje. Standardní elektrodové potenciály se v tabulkách obvykle uvádějí jako redukce, takže hodnota E0 pro oxidaci zinku musí být vynásobena -1. Obě poloreakce pak dohromady tvoří celkový potenciál reakce. V tomto případě je E0Zn/Zn2+ = +0.76 V (po obrácení znaménka) a E0Cu2+/Cu = +0.34 V. Celkový rozdíl potenciálů tedy činí +1.1 V. Pro reakci (11) probíhající ve standardních podmínkách je celkový potenciálový rozdíl kladný, což znamená, že ΔG (v našem případě ΔG0) je záporné a reakce bude probíhat spontánně. Za nestandardních podmínek musíme použít úplnou Nernstovu rovnici pro obě poloreakce.
Kinetika
Zatímco termodynamika se pokouší odpovídat na otázku, zda je reakce termodynamicky uskutečnitelná, reakční kinetika se zabývá tím, jakou rychlostí a zda vůbec bude taková reakce probíhat.
Existuje mnoho termodynamicky příznivých reakcí, jež ale spontánně neprobíhají. Všichni vědí, že hoření dřeva ve vzduchu uvolňuje velké množství energie, kterou lze proměnit na práci. Oxidace celulózy dřeva kyslíkem na vodu a oxid uhličitý musí mít negativní hodnoty ΔG. Jak to, že v naší atmosféře bohaté na kyslík vůbec ještě nějaké lesy stojí?
Podobně diamanty, často považované za „věčně trvající”, jsou termodynamicky nestálé modifikace grafitu či sazí.
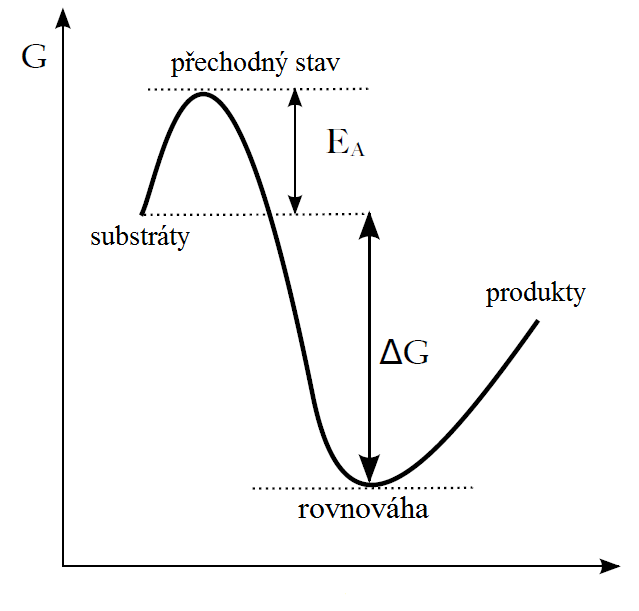
Některé reakce mohou být termodynamicky uskutečnitelné, ale kineticky nepravděpodobné. Tento fenomén nazývaný kinetická bariéra zapříčiňuje existence nestálých přechodných stavů (aktivovaných komplexů), jež se vytvoří jen při dodání většího množství energie (vznik aktivovaného komplexu je termodynamicky nepříznivý). Tato dodatečná energie se nazývá aktivační energie (EA).
Reakční rychlost
Aby mohly spolu dvě či více látek reagovat, musí dojít ke srážce jejich molekul. Pravděpodobnost srážky se zvyšuje s rostoucí teplotou, tlakem a koncentrací látek.
Reakční rychlost (v) můžeme definovat jako rychlost úbytku reaktantů či rychlost přírůstku produktů:
Jak spolu koncentrace reaktantů a rychlost průběhu reakce souvisí? Mějme jednoduchou reakci X → Y. Rychlost této reakce bude úměrná [X] podle rovnice:
v = – d[X] / dt = k[X] (15)
kde k = rychlostní konstanta. Rychlost ale může být úměrná [X]2 nebo nemusí být úměrná [X] vůbec – v takovém případě probíhá reakce konstantní rychlostí. Přesný vztah mezi reakční rychlostí a koncentrací reaktantů je empirický fakt a nedá se odvodit ze stechiometrie. Chemici definují kinetický řád reakce na základě počtu členů, jejichž koncentrace ovlivňují její rychlost. Pokud mezi nimi vztah neexistuje, a tedy platí rovnice v = k, hovoříme o řádu nultém. Je-li rychlost přímo úměrná koncentraci jednoho z reaktantů, jedná se o kinetiku prvního řádu (jako v případě výše uvedené reakce (15)). Jestliže je rychlost ovlivněna koncentrací dvou reaktantů nebo se jedná o exponenciální vztah jednoho reaktantu (v = k [X][Y] nebo v = k[X]2), hovoříme o kinetice druhého řádu atd.
Někdy chceme předpovědět, jaké množství reaktantu X zůstane nezreagováno po čase t od začátku reakce, nebo jak dlouho potrvá, aby [X] klesla na polovinu. Při reakcích nultého řádu je výpočet jednoduchý, ale pro řády vyšší se výpočet komplikuje. Pro reakci prvního řádu platí:
– d[X] / dt = k[X] (16)
rovnici zintegrujeme:
-(1/[X]) d[X] / dt = k[X]
– ∫ (1/[X]) d[X] / dt = k[X]
– ∫ (1/[X]) d[X] / dt = ∫ k[X]
-ln[X] = kt + c (17)
a řešení pro t = 0 (kdy [X] = [X]0):
c = – ln[X0] (18)
-ln[X] = kt – ln[X0]
-ln[X] + ln[X0] = kt
-ln[X] / [X0] = kt
[X] / [X0] = e-kt
[X] =[X0] e-kt (19)
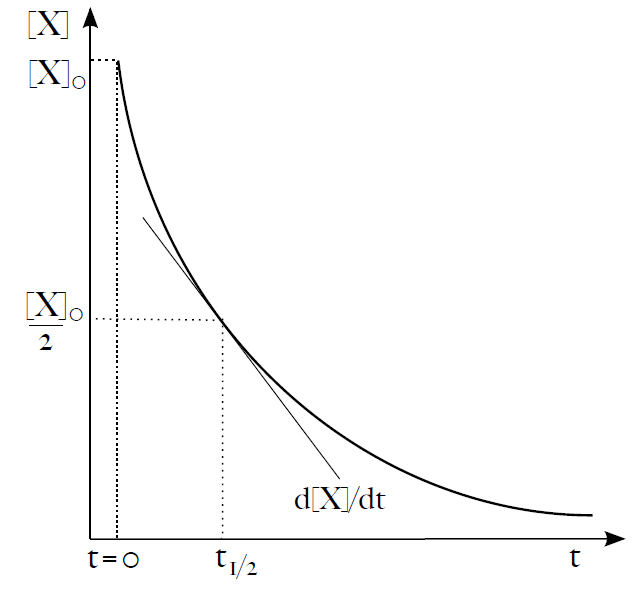
Tato rovnice popisuje exponenciální nárůst koncentrace X v čase. Užitečným parametrem exponenciálního rozkladu je čas potřebný na snížení počáteční koncentrace (či množství) látky X na polovinu. Nazývá se poločas (t1/2). Z rovnice (19) můžeme poločas vyjádřit jako:
t1/2 = ln2/k
Autor podkapitoly: Jan Trnka